OpenTerrain

In this project page we describe the use of the EGM (the Earth Geodetic Model) for correcting the altitude of a GPS sensor.

The Use Case

When you used a GPS sensor at the beach, you might have wondered why the sensor shows an altitude of something like 50 meters but not 0 meters above mean sea level.

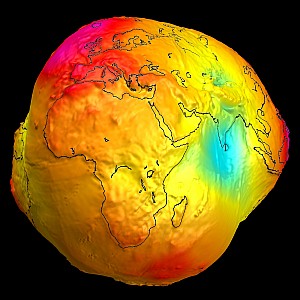
This is because the sensor gives the relative height difference to the so called WGS84 ellipsoid. The ellipsoid is an approximation of the earth’s shape. In reality the shape of the earth, that is the sea surface, is not an exact ellipsoid, but rather a deformed ellipsoid with undulations, more or less a potato:

The undulated surface is called the geoid. The undulations are caused by gravitational anomalies, which attract the water body and form swells over areas of higher gravity. The swells can be up to 86 meters high and the troughs can be up to 107 meters deep. The following image shows an exaggerated view of the earth’s “potato” shape.

Deutsches Zentrum für Luft- und Raumfahrt (DLR)

The uncorrected coordinates of the GPS device do not account for those undulations, so the beach can be within ±100 meter above the ellipsoid. In the following we come up with a handy solution to correct the GPS altitude so that it reflects the elevation above the mean sea level.

The EGM Data

The EGM08 DEM data set describes the earth’s geoid with a resolution of either 1 or 2.5 arcmin resolution. It is provided as a digital elevation model (DEM) by the National Geospatial-Intelligence Agency (NGA). The latest WGS84 ‘08 version is available from here:

The format of the 2.5arcmin DEM grid is lsb-first floating point raw data with 8640 columns and 4321 rows:

In the following we would like to transform the above raw DEM into a GeoTiff file using GDAL utilities:

1) We uncompress the data and rename it to EGM08_25.bil (ESRI raw file format).

2) We add an ESRI header file EGM08_25.hdr with the following contents (defining the respective Lat/Lon image coverage):

ncols 8640
nrows 4321
cellsize 0.041666666666666667
xllcorner -0.020833333333333333
yllcorner -90.020833333333333333
nodata_value -9999
nbits 32
pixeltype float
byteorder lsbfirst

3) We add a ESRI projection file EGM08_25.prj with the following contents (defining a standard WGS84 geographic projection):

GEOGCS["WGS 84",DATUM["WGS_1984",SPHEROID["WGS 84",6378137,298.257223563,
AUTHORITY["EPSG",7030]],TOWGS84[0,0,0,0,0,0,0],AUTHORITY["EPSG",6326]],
PRIMEM["Greenwich",0,AUTHORITY["EPSG",8901]],UNIT["DMSH",0.0174532925199433,
AUTHORITY["EPSG",9108]],AXIS["Lat",NORTH],AXIS["Long",EAST],AUTHORITY["EPSG",4326]]

4) Now we can use the gdal_translate utility to transform the raw data into a GeoTiff:

gdal_translate EGM08_25.bil EGM08_25.tif

Unfortunately, this does not work, because the original data contains 4 padding bytes at the left and right end of each row, meaning that the first and last columns of the data just contain irrelevant padding data, which we need to strip off. The cell padding is in fact an “undocumented” feature of the EGM08 raw data, there is no reliable information about it in the README.

Fixing the EGM Data

Since the raw data is padded, we need to fix the EGM08 data by stripping off the first and last column. We start with 8642 columns and end up having 8640. We also repeat the first column as last one to get a full 360 degrees of coverage. We do so with the following small C++ program, producing a 8641×4321 data set:

With the fixed output file we repeat steps 1) to 4), except that we need to take into account that we now have 8641×4321 cells:

ncols 8641
nrows 4321
cellsize 0.041666666666666667
xllcorner -0.020833333333333333
yllcorner -90.020833333333333333
nodata_value -9999
nbits 32
pixeltype float
byteorder lsbfirst

Visualizing the EGM Data

Finally, we color-map the height field to a RGB image using the gdaldem utility. For that purpose we create a color-map file EGM08_25.txt with the following contents:

-200 0 0 0
-100 255 0 0
100 0 0 255
200 255 255 255

And run the gdaldem utility:

gdaldem color-relief EGM08_25.tif EGM08_25.txt EGM08_25_relief.tif

This yields the following (contrast-enhanced and down-sized) result:

Red values represent troughs of the geoid (negative values of the geoid DEM), whereas blue values represent hills (positive values of the geoid DEM).

The fixed EGM data and the GeoTiff image can be downloaded from my mirror server:

The EGM Representation

The EGM08 geotiff file is about 150 MB in total. That’s too large to include into an Android app so that it is able to correct the GPS altitudes. On the other hand, it is sufficient to have the geoid heights with about 1 meter accuracy, because the vertical precision of a [non-differential] GPS device is inherently worse than that (more like ±10m in my experience). Therefore, we may down-sample the EGM data to a more reasonable size of, say, 181×91 grid points. We do so with libGrid’s grid2c tool:

grid2c EGM08_25.tif Geoid-181x91.c 181 91

The grid2c program outputs the data as C++ source code in which a corresponding float matrix is defined, so that it can be included as a regular module into a C++ program.

For example, the C++ output for a 11×6 geoid matrix is:

static const int size_x=11;
static const int size_y=6;

static const double LLWGS84_swx=0;
static const double LLWGS84_swy=-90;
static const double LLWGS84_nwx=0;
static const double LLWGS84_nwy=90;
static const double LLWGS84_nex=360;
static const double LLWGS84_ney=90;
static const double LLWGS84_sex=360;
static const double LLWGS84_sey=-90;

static const float data[size_y][size_x]={
   -30.15,-30.15,-30.15,-30.15,-30.15,-30.15,-30.15,-30.15,-30.15,-30.15,-30.15,
   22.8511,40.7621,22.669,-11.7373,-11.8084,-7.656,-12.5149,-8.93637,0.880717,0.00731354,22.8511,
   17.0403,-33.2788,-73.6445,15.6048,45.5325,27.1284,5.36011,-8.95659,-6.25443,-17.5287,17.0403,
   18.9033,-25.0505,-76.6696,13.3805,39.3692,20.335,-0.984197,-13.8498,-0.883649,-20.8845,18.9033,
   47.2155,10.0123,-37.2059,-3.50886,2.8773,-1.61806,-7.87575,-27.4857,-22.7701,37.2808,47.2155,
   14.8985,14.8985,14.8985,14.8985,14.8985,14.8985,14.8985,14.8985,14.8985,14.8985,14.8985
};

The 181×91 cell C++ source is too large to show here as plain text, it is available on my server:

The EGM Interpolation

To correct the GPS altitude we need to interpolate the above data matrix at a specific latitude and longitude. This yields the geoid height at the corresponding location. Then we subtract the geoid height from the GPS altitude and end up having the true elevation above sea-level, hurray! In order to avoid misunderstandings this elevation is often abbreviated as m.a.s.l. meaning meters above sea level.

To interpolate the grid we use the following bi-linear interpolation code:

The interpolation function requires the 2D interpolation position as parameter in normalized coordinates (meaning a range of [0..1]). Therefore, we map the geographic position, defined by latitude and longitude, to normalized coordinates nx and ny and interpolate at (nx, ny):

The Full EGM Source Code

Putting the pieces together, we get the following source code for the 11×6 EGM grid interpolation:

Testing

The above program outputs the following result:

The geoid height at Porto Vecchio at lat/lon = 41.6/9.3 is 45.4257m.

Let’s see if we made a mistake - let’s compare the result of 45.4257m at lat/lon = 41.6/9.3 (using the down-sampled 11×6 grid) with the result of the online geoid calculator (using the full-res grid):

We get a reference value of 48.7170 meters, which is about 3 meter off. But hey, that’s the result for the 11×6 grid. Repeating the same procedure with the 181×91 grid yields:

That’s a difference of 3cm, which is pretty well within our goal of 1 meter accuracy :-)

Mission completed, GPS measurements can be corrected on-the-fly using the above C++ code!

Full source code is here:

Please do me a favour: If you happen to use the above code, please drop me a note and link to this page!